Context
La société MegaSecure vient d’éditer une mise à jour de sécurité pour leurs serveurs. Après analyse de la mise à jour, vous vous apercevez que l’éditeur utilise maintenant ce code pour l’exponentiation :
1
2
3
4
5
6
7
8
9
10
unsigned long exp_by_squaring(unsigned long x, unsigned long n) {
// n est l'exposant secret
if (n == 0) {
return 1;
} else if (n % 2 == 0) {
return exp_by_squaring(x * x, n / 2);
} else {
return x * exp_by_squaring(x * x, (n - 1) / 2);
}
}
Vous avez accès à un serveur où vous avez pu lancer en tant qu’utilisateur exp_by_squaring(2, 2727955623) tout en mesurant sa consommation d’énergie. L’exposant ici est donc n = 2727955623, soit 10100010100110010100110010100111 en binaire. Cette trace de consommation est sauvegardée dans trace_utilisateur.csv.
Vous avez également réussi à mesurer la consommation d’énergie pendant l’exponentiation d’une donnée de l’administrateur. Cette trace de consommation est sauvegardée dans trace_admin.csv. Saurez-vous retrouver son exposant secret n ?
Le flag est au format FCSC{1234567890} avec 1234567890 à remplacer par l’exposant secret de l’administrateur écrit en décimal.
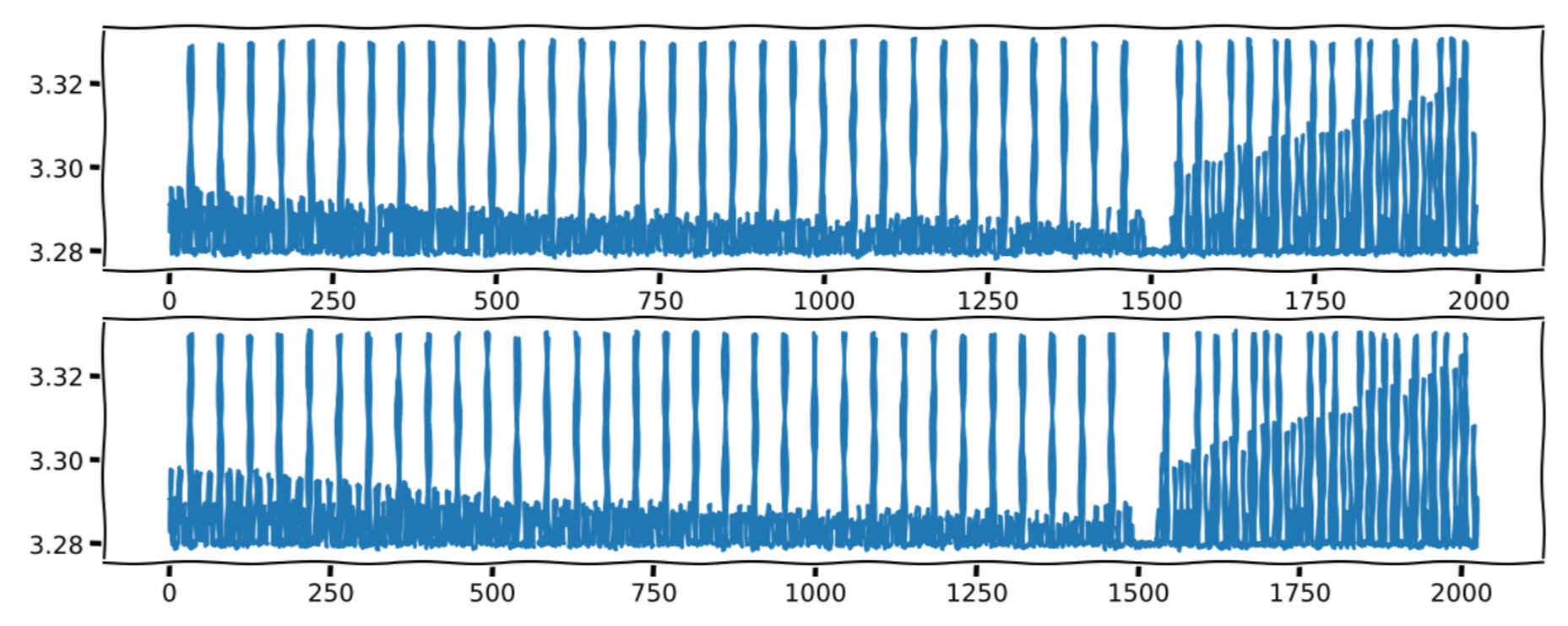
We are given:
- the user trace (trace_utilisateur.csv)
- the admin trace (trace_admin.csv)
- the above image with the user trace above and the admin trace below
Let’s take a look at the code:
1
2
3
4
5
6
7
8
9
10
unsigned long exp_by_squaring(unsigned long x, unsigned long n) {
// n est l'exposant secret
if (n == 0) {
return 1;
} else if (n % 2 == 0) {
return exp_by_squaring(x * x, n / 2);
} else {
return x * exp_by_squaring(x * x, (n - 1) / 2);
}
}
It will have 2 stages. First going decreasing n through recursive descent. Then when n == 0, we go back through backtracking to get the result.
We can see the phases on the image given. The first one is always the same patern. The second one is different.
We know that a multiplication consumes a lot of power. So, whenever we see a big peek in power consumption, it’s because a multiplication has been made.
Another interesting thing:
With each recursion, we divide n by 2 so we handle on bit in the binary representation since binary is base 2.
Example:
13 in decimal is 1101 in binary.
at first recurence, n is odd so n becomes (n-1) / 2 = (12 - 1) / 2 = 6
6 in decimal is 110 in binary so we handled the bit on the right.
6 is even so it become n / 2 = 6 / 2 = 3
3 in decimal is 11 in binary so we handled the bit on the right.
and so on..
There will be as many recursion as there is number of digits in the input in binary representation.
So there will be 32 recursions.
First stage:
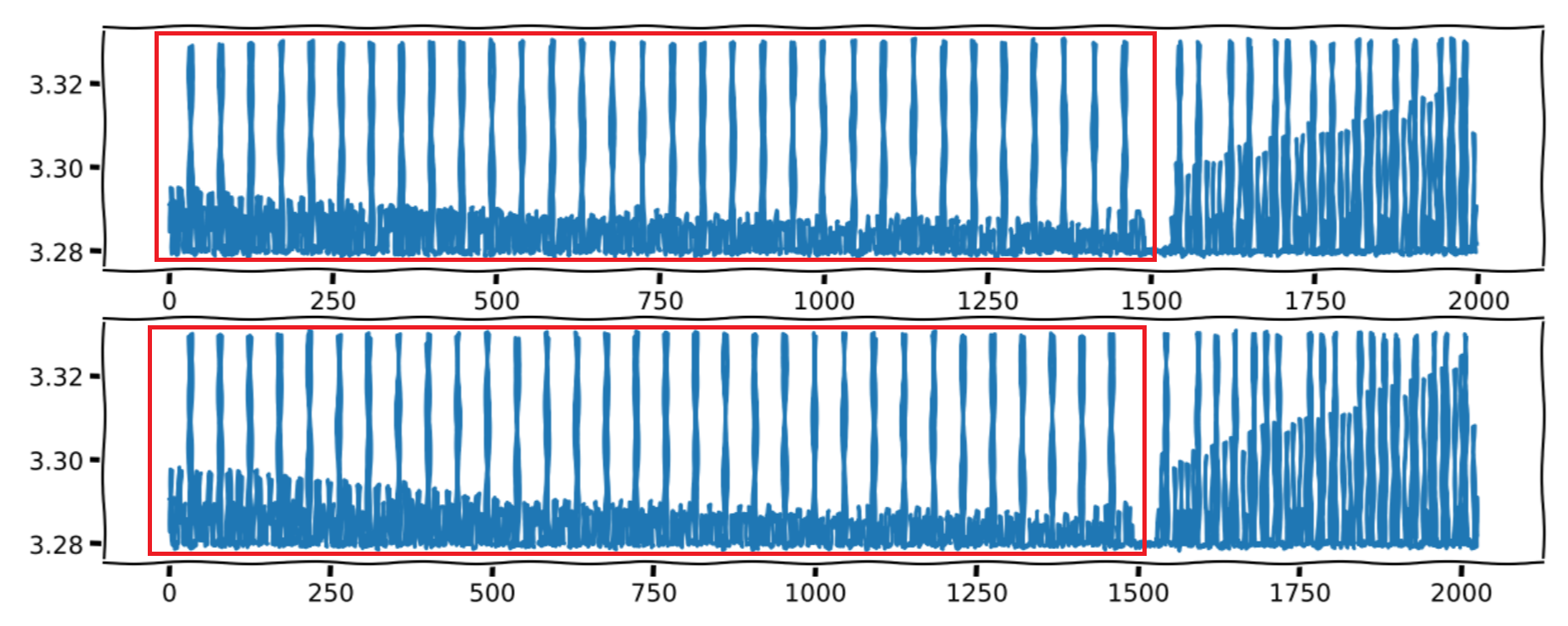
The first stage is the recursive descent. In this stage, no matter if n is odd or even, we will do one multiplication:
1
2
3
4
5
// if n is even
exp_by_squaring(x * x, n / 2)
// if n is odd
exp_by_squaring(x * x, (n-1) / 2)
That’s why we see 32 peeks in the first stage. One peek per multiplication, 1 multiplication per recursion, 32 recursions.
We are handling bits from right to left.
Second stage:
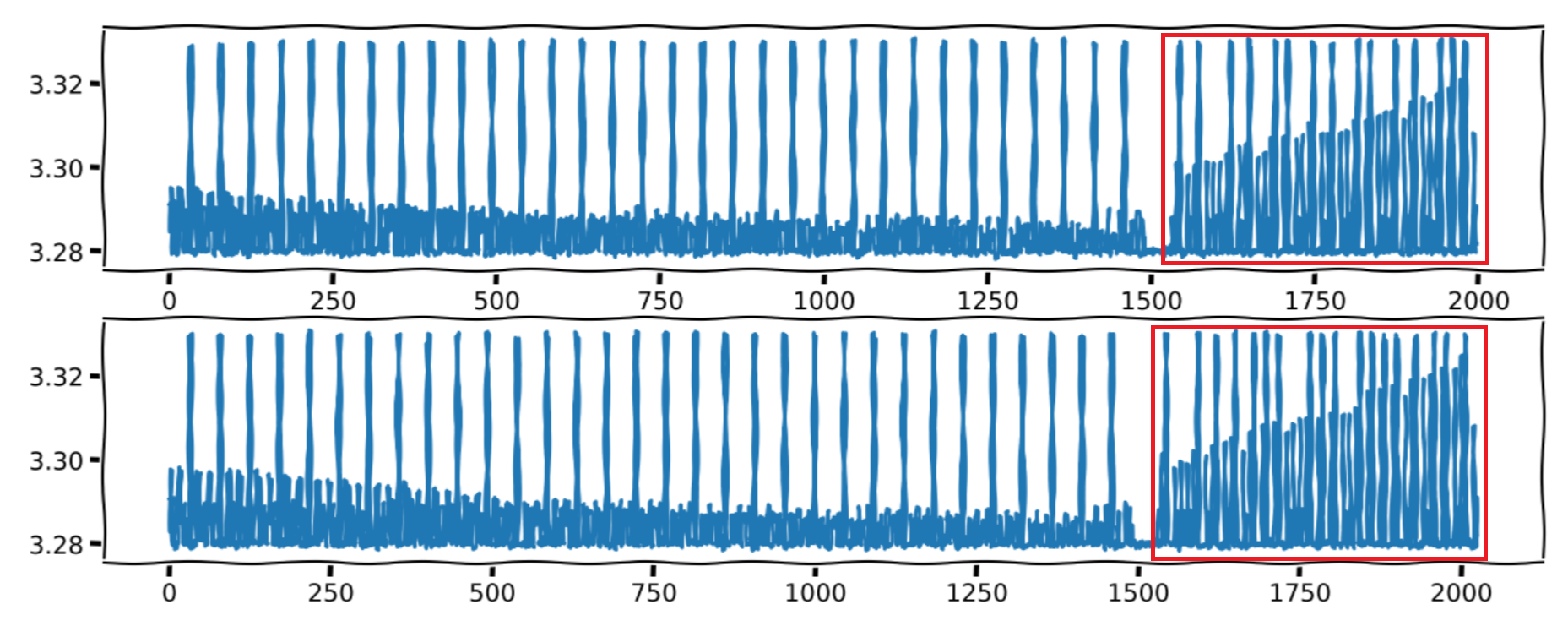
This stage is the backtracking of the recursion.
In this stage, if n is even there is no multiplication. If n is odd, there is a multiplication. So we only have a peek if n is odd (1).
1
2
3
4
5
6
7
// exp_by_squaring(...) has been calculated during the recursive descent.
// if n is even, no multiplication
exp_by_squaring(x * x, (n - 1) / 2)
// if n is odd, one multiplication
x * exp_by_squaring(x * x, (n - 1) / 2)
Since it is backtracking, we handle the digits in reverse order from the first stage (from left to right).
If we take a look at the user trace, it begins with a peek so the first digit is 1. Then there is a little peek so it’s 0. Then there is a big peek so it’s 1 and so one.
The binary representation of the user number is 10100010100110010100110010100111. It begins with 101 (left to right) as expected.
Now that we know how find the n from the trace, we can find the admin number 😏.
admin number: 10001010101110001110011110101101
We’ve got the flag: FCSC{10001010101110001110011110101101}
I hope you enjoyed this explaination and that it could be useful in the future 😊.